leetcode 1024 Stone Game II (DP, Java)

문제 링크

문제 요약

n(<= 100) 개의 돌무더기들이 주어집니다.

[2,7,9,4,4]

A, B 가 있으면 게임을 합니다.

게임의 내용은 턴제 게임으로 자신의 턴일 때 마다 돌무더기를 가져갑니다.
각 턴에 가져올 수 있는 돌무더기의 수는 (1 <= x <= 2*m) 입니다.
다음 턴이 될 때 m 은 max(m, x) 로 최신화됩니다.

A, B 는 각자 자신의 턴에 최선의 수를 판단합니다.

문제 풀이

이 문제는 DP 문제이다. 어떻게 판단할 수 있을까요.. 처음 문제를 읽었을 땐 이게 어떤 유형의 문제인지 감이 안잡힐 것입니다.

이럴땐 먼저 brute force 로 접근하는 것입니다.

private int rec(int i, int m, int n, int[] suffixSum) {
    if (i + 2 * m >= n) return suffixSum[i];

    int result = 0;
    for (int j = 1; j <= 2 * m; j++) {
        result = Math.max(result, suffixSum[i] - rec(i + j, Math.max(m, j), n, cache, suffixSum));       
    }

    return result;
}

이러한 로직을 기대할 수 있습니다. 현재 로직에선 구간합을 빠르게 조회하기 위해 suffixSum(prefixSum) 을 사용하고 있습니다.

또 눈여겨볼 부분은 다음 부분 같습니다.

suffixSum[i] - rec(i + j, Math.max(m, j), n, cache, suffixSum)

(현재 구간에서 얻을 수 있는 모든 값 - 다음 구간에서 얻을 수 있는 최선의 값)

다음 구간에서 얻을 수 있는 최선의 값 을 빼주는 것은 이 값이 다음 구간 즉, 상대 턴에서 얻게되는 최선의 값이기 때문입니다.

이러한 논리로 재귀적 접근하여 해결하는 것입니다.

하지만 소요되는 시간이 너무 많습니다. n <= 100.

이제 여기서 subproblem 으로 나눌 수 있을지 고민을 해야합니다.

나눌 수 있다면 DP로 해결할 가능성이 높아집니다. 그리고 아래 이미지와 같이 중복되는 경우가 잇습니다.

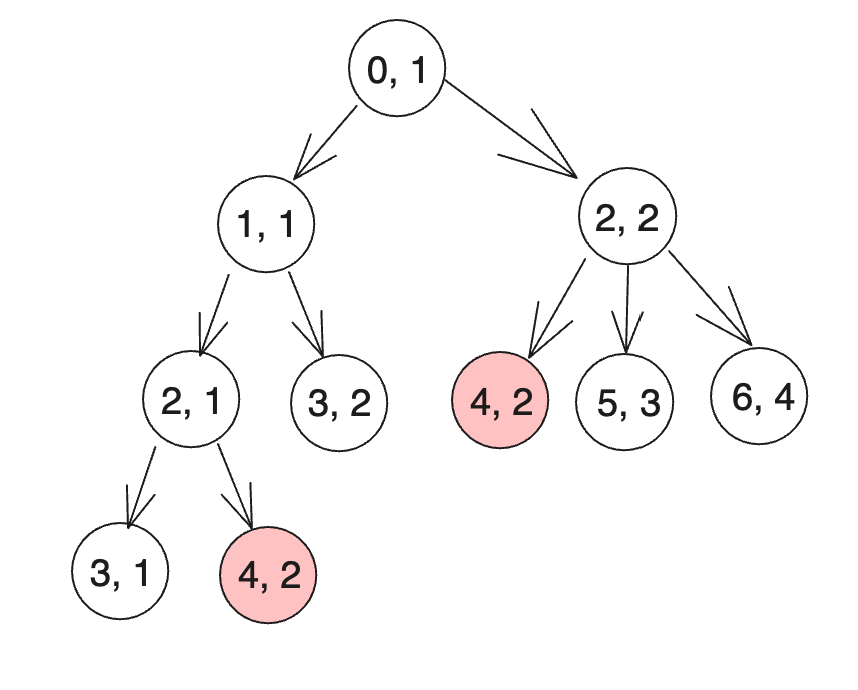
이제 이에 대해 메모이제이션을 하면 성능개선을 할 수 있습니다.

TopDown 방식을 통해 DP 로직을 구현했다면 여기서 얻은 점화식을 토대로 BottomUp 방식으로도 구현할 수 있습니다. 가능하다면 두 방식으로도 다 구현을 해야 공부하는데 도움이 되는 것 같습니다.

소스코드 Java

import java.util.*;

class Solution {
    public int stoneGameII(int[] piles) {
        int n = piles.length;

        int[][] cache = new int[n][n + 1];
        int[] suffixSum = Arrays.copyOf(piles, n);

        for (int i = n - 2; i >= 0; i--) {
            suffixSum[i] += suffixSum[i + 1];
        }

        return rec(0, 1, n, cache, suffixSum);
    }

    private int rec(int i, int m, int n, int[][] cache, int[] suffixSum) {
        if (i + 2 * m >= n) return suffixSum[i];

        if (cache[i][m] != 0) return cache[i][m];

        for (int j = 1; j <= 2 * m; j++) {
            cache[i][m] = Math.max(cache[i][m], suffixSum[i] - rec(i + j, Math.max(m, j), n, cache, suffixSum));       
        }

        return cache[i][m];
    }
}


class Solution {
    public int stoneGameII(int[] piles) {
        int n = piles.length;

        int[][] cache = new int[n][n + 1];
        int[] suffixSum = Arrays.copyOf(piles, n);

        for (int i = n - 2; i >= 0; i--) {
            suffixSum[i] += suffixSum[i + 1];
        }

        for (int i = n - 1; i >= 0; i--) {
            for (int j = 1; j <= n; j++) {
                if (i + 2 * j >= n) {
                    cache[i][j] = suffixSum[i];
                } else {
                    for (int k = 1; k <= 2 * j; k++) {
                        cache[i][j] = Math.max(cache[i][j], suffixSum[i] - cache[i + k][Math.max(j, k)]);
                    }
                }
            }
        }

        return cache[0][1];
    }
}